Noise Schedule

In Diffusion Models, the noise schedule dictates how much noise is added to the data at each time step. The noise schedule is typically defined as a function $\alpha_t$ that maps a time step $t$ into a value $\alpha_t \in [0, 1]$. Modular Diffusion comes with a growing set of prebuilt noise schedules.

Constant schedule

Constant noise schedule given by $\alpha_t = k$.

Parameters

• steps -> Number of time steps $T$.
• value -> Constant value $k$.

Example

from diffusion.schedule import Constant

schedule = Constant(1000, 0.995)

Visualization

Applying Gaussian noise to an image using the Constant schedule with $T=1000$ and $k=0.995$ in equally spaced snapshots:

Linear schedule

Linear noise schedule introduced in Ho et al. (2020) computed by linearly interpolating from $\alpha_0$ to $\alpha_T$.

Parameters

• steps -> Number of time steps $T$.
• start -> Start value $\alpha_0$.
• end -> End value $\alpha_T$.

Example

from diffusion.schedule import Linear

schedule = Linear(1000, 0.9999, 0.98)

Visualization

Applying Gaussian noise to an image using the Linear schedule with $T=1000$, $\alpha_0=0.9999$ and $\alpha_T=0.98$ in equally spaced snapshots:

Cosine schedule

Cosine noise schedule introduced in Nichol et al. (2021) which offers a more gradual noising process relative to the linear schedule. It is defined as $\alpha_t = \frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$, where:

• $\bar{\alpha}_t=\frac{f(t)}{f(0)}$
• $f(t) = \cos(\frac{t/T+s}{1+s} \cdot \frac{\pi}{2})^e$

Parameters

• steps -> Number of time steps $T$.
• offset (default: 8e-3) -> Offset $s$.
• exponent (default: 2) -> Exponent $e$.

Example

from diffusion.schedule import Cosine

schedule = Cosine(1000)

Visualization

Applying Gaussian noise to an image using the Cosine schedule with $T=1000$, $s=8e-3$ and $e=2$ in equally spaced snapshots:

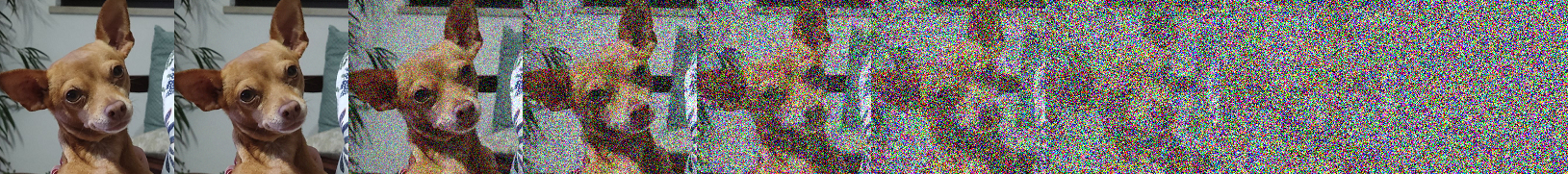
Square root schedule

Square root noise schedule introduced in Li et al. (2022). It is defined as $\alpha_t = \frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}$, where $\bar{\alpha}_t=1-\sqrt{t/T+s}$.

Parameters

• steps -> Number of time steps $T$.
• offset (default: 8e-3) -> Offset $s$.

Example

from diffusion.schedule import Sqrt

schedule = Sqrt(1000)

Visualization

Applying Gaussian noise to an image using the Sqrt schedule with $T=1000$ and $s=8e-3$ in equally spaced snapshots:

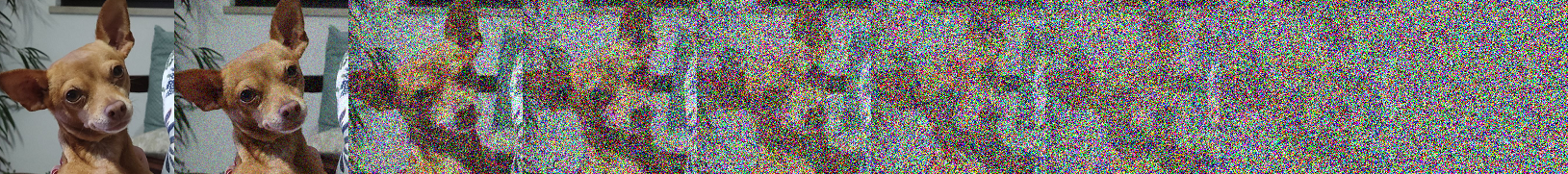
If you spot any typo or technical imprecision, please submit an issue or pull request to the library's GitHub repository .